このレポートは、かたつむりNo.324[2009(平成21)2.8]に掲載されました

戻る

地球の大きさを計る（１）
－紀元前230年　アレクサンドリアにて－
運営委員　高　木　茂　行
 
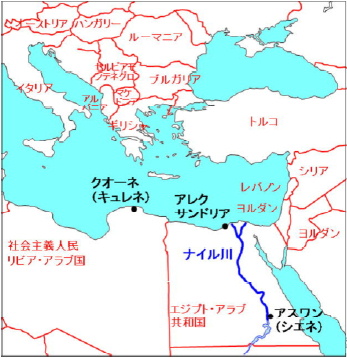
ヨーロッパ・アフリカ地図
図１　ヨーロッパ・アフリカ地図
太陽が作る影
図２　太陽が作る影
アレクサンドリアとシエネと太陽の位置
図３　アレクサンドリアとシエネと太陽の位置
地球の大きさの計算
図４　地球の大きさの計算
　中学の教科書のコラムに『紀元前に地球の大きさを測ったギリシャの人』が紹介されていた。 読んだのは30年以上も前のことだったが、古い時代に地球の大きさをかなり正確に測定したことが印象に残っていた。 先日図書館に行き、これに関する記事を見つけ改めて感心した。 今回のかたつむりでは、このギリシャ人の測定、日本で最初に地球の大きさを測った人、同じ方法でトライした結果について紹介する。 原稿を書こうとインターネットを調べていたら「カーナビで地球の大きさを測る」という山本先生のホームページにヒットした1)。 こちらも、ぜひ、見ていただきたい。
　地球の大きさが測られたのは紀元前230年だった。 西暦ではキリストが生まれた年を0年とし、それ以前を紀元前で表すから今から約2240年前のことだ。 測定を行ったのはアフリカの町キュレネ（現在のクオーネ）で生まれたエラストテネス2)。
　計測が行われた場所はアレクサンドリアだった（図１）。この頃は、ギリシャの文明がヨーロッパからアフリカに広がっていた。 それらの都市の中でもっとも栄えたのがアレクサンドリアで、ギリシャ文明の知識を集大成した図書館が作られていた。 エラストテネスは才能を認められ、この図書館の館長となっていた。
　そんなエラストテネスは、『シエネ（現在のアスワン）の町では、夏至の日に井戸にはまっすぐ陽が差す』ことを文献で知り、 地球の大きさが分かると喜んだという3),4)。彼は次のことを知っていた。
① アレクサンドリアはシエネの町からほぼ南にある。
② アレクサンドリアとシエネとの距離は5000スタジア （１スタジアは当時の距離の単位で0.185km。5000スタジアは0.185×5000で925km）
エラストテネスはどうやって、地球の大きさを測ったのだろうか？
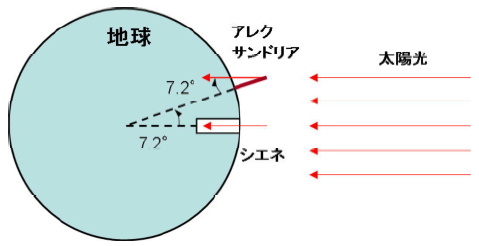
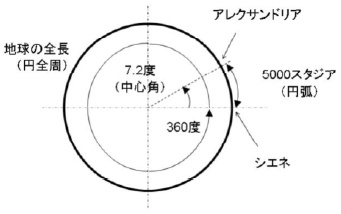
　これだけのことで地球の計り方が思いつく団員は、将来に科学者として大成することだろう。 エラストテネスは、同じ夏至の日にアレクサンドリアで、棒が作る影から太陽の角度を調べた。 図２のように棒に太陽が当たると影ができる、これを調べたのである。 実際に計ってみると短い影ができ、太陽は垂直から7.2度傾いていた。 一方、シエネの町では井戸にまっすぐ陽が指すので影はできず、太陽の角度は地面に垂直となる。 これを図で表すと、図３のようになる。 シエネは太陽が垂直に射す位置にあり、アレクサンドリアは7.2度傾いた位置にある。 算数の得意な団員なら、地球の大きさが計算できるだろう。
　計算を分かりやすくするため、図３を図４のように書き直した。計算に使う考えは、
『円弧（円の一部）の長さは、中心角に比例する』
ということだ。簡単な例として、全周が100mmで中心角が90°の円弧の長さを考える。 円全周の角度は360°なので、90°は全周の90／360＝1／4となる。 円弧の長さは中心角に比例して全周の1／4だから、円弧の長さは100mm÷4＝25mmとなる。 これを式で表せば、
円弧の長さ　＝　全周の長さ　×　中心角　÷　360
となる。全周の長さが求まるように書き直すと
全周の長さ　＝　円弧長さ　×　360　÷　中心角
となる。
　エラストテネスの場合は中心角が7.2°、円弧の長さが5000スタジア（925km）であるから、次のような計算となる。
地球の大きさ（全周）＝925km×360°÷7.2°＝46250km
現在の最先端の測定で地球の大きさは40008km となっているので、かなりの精度で測定できたことになる。
　2000 年以上も昔に地球の大きさを計ったエラストテネスには驚く。 さて、日本でも同じような測定が行われたが、それは江戸時代のことだった。次回のかたつむりでその人を紹介する。 多くの団員が知っている有名な人物だ。



（つづく）
１）山本明利： カーナビで地球の大きさを測る
２）世界大百科事典：　平凡社，３巻，658～659（1992）
３）大浜一之：地球の雑学辞典，日本実業出版社，18～19（1990）
４）財団法人地図情報センター ：エラトステネスはこうやって地球の大きさを測った
※このページから、地図・地理知識（現在一部オープン）／地図学博物館にある「当センター所蔵旧地形図の部屋」 のリンクより［バーチャル地図学博物館］を開くと「地図の歴史の部屋」へ移動することができます。 （2009/2/18現在工事中）
このページのギリシア、ローマ時代の地図にある「どうやって測定したかはこちら」のリンクより ［エラトステネスはこうやって地球の大きさを測った］へ移動することができます。


山本先生のＨＰから一部転載しました（無断でごめんなさい・・・事務局）

　さて、お話かわって現代。 ＧＰＳ（Global Positioning System）衛星が発する電波を受信して空間での三次元位置を決定できる装置が 民生品としても普及してきました。 カーナビゲーションシステムやポータブルＧＰＳ受信機が手ごろな価格で入手できるようになってきたのです。 カーナビはCD-ROMに記録された地図情報と重ね合わせて自車位置を地図上に表示し、道案内までしてくれます。 カーナビは基本的には自車の緯度経度を算出し、それを地図上に投影していますから、 ボタン一つで緯度経度を表示させることも可能です。 精度は角度で１～３秒、距離にして30～100ｍ程度です。 そこで、カーナビを積んだ車を南北に走らせて緯度の変化を測定すると共に、距離を走行距離計で測れば、 エラトステネスの方法で簡単に地球の大きさを計算することができます。（中略）
　下の表と図は藤沢市から大和市をぬけて南北にのびる県道４６７号藤沢町田線に沿って車を走らせて測定したデータです。 使用したカーナビはカシオのＮＳ－７７０です。 善行の教育センター前からダイクマ大和店の駐車場まで11.8kmを往復しながら測定したデータは、ぴったり直線に乗ります。 直線を外挿すると距離14kmあたりの緯度差は7.5分と読めます。これから地球の全周を求めると 　地球全周＝14km×(360×60)/7.5＝40320km　となります。 なかなかの精度ですね。データの直線性のよさを考えると、10km以上も車を走らせる必要はなかったようです。 ポータブルのＧＰＳ受信機があれば、生徒と共に学校のそばを１kmも散歩するだけで地球の大きさは求まってしまいます。 すごい時代になったものです。



戻る