このレポートは、かたつむりNo.328[2009(平成21)5.17]に掲載されました
 戻る
戻る
| 地球の大きさを計る(4) | ||||||||||||||
| - メジャーを持って地球の大きさを計ってみよう - | ||||||||||||||
| 運営委員 高 木 茂 行 | ||||||||||||||
地球の大きさを測るには、2点の距離と緯度差あるいは太陽の見える角度を測ればよい。 エラストテネスは、人から聞いたか調べたりしてアレクサンドリアとシエナの距離を知っていた。 太陽の見える角度をアレクサンドリアで測定した。伊能忠敬は二点間の距離を歩いて計り、角度を星の角度から求めた。 僕らにもできそうな方法として、
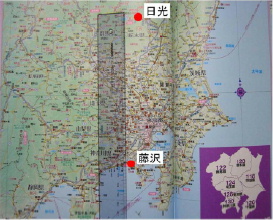
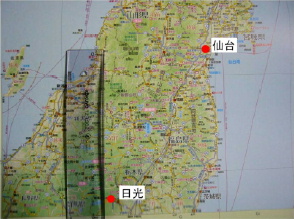
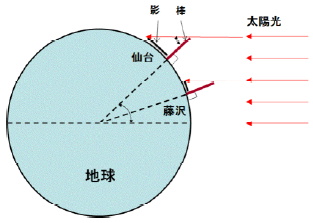
昨年の秋に仙台(図1)に行った時に、この方法を試した。測定地は、自宅近く(藤沢市城南)と仙台駅の近くの2点。 ①は『なるほど日本知図帳』1)を使って測定した。 藤沢と仙台が1枚に書かれたちょうど良い図が無かったので、藤沢-日光と日光-仙台とに分けた。 藤沢と日光との距離は、図2のように定規で測定し、長さは156.5mとなった。 縮尺が1,000,000対1なので実際の長さは、156.5mm×1,000,000=156500000mm=156500m=156.5kmと求まった。 同様に日光から仙台までの南北方向の距離も図3のように測定し、縮尺をかけて165 kmとなった。 この時、距離と角度ともに南北方向のみを議論しているので、藤沢から定規を真北に向けて南北方向の距離に着目した。 藤沢から仙台までの南北方向の距離は、合計して321.5kmとなった。 次に、②の太陽の角度は地上に立てられた棒の高さと影の長さから計ることにした。 図4のように太陽の光を受けると、緯度によって影の長さが違ってくる。 緯度が高い仙台では藤沢より影が長くなる。 棒が地面に対し垂直に立っていると考えれば、棒と影の部分を2辺とする直角三角形ができる。 それぞれの辺の長さを一定の割合で小さくして、直角三角形を書いて(A)の角度を測れば太陽の見える角度を求める。
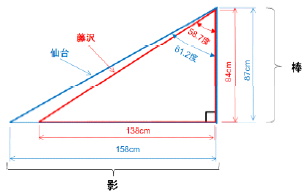
この結果から各辺の長さを10分の1とし、図7のように直角三角形を作図した。赤が藤沢、青が仙台で計った結果である。 2つの三角形の角度は仙台で61.2°、藤沢で57.8度となり、角度差は2.49°となった。 2点間の距離は地図を使って321.5kmと計算されている。地球の大きさは2月のかたつむりに書いたように、
全周の長さ= 円弧長さ× 360 ÷ 中心角
で求められる。円弧の長さにあたるのが321.5kmで中心角が2.49°なので、
2点間の距離は地図を使って321.5kmと計算されている。地球の大きさは2月のかたつむりに書いたように、
全周の長さ= 321.5km×360°÷ 2.49°
となった。実際の地球の大きさは、最新の測定では40008kmされている。
今回の測定では、藤沢と仙台の東西方向(経度)なども考慮していないし、地図上の距離も定規を横にあてて計っている。
荒っぽい測定ではあるが、簡単な道具で地球の大きさを誤差15%の精度で測ることができた。=46482km 団員の皆さんも東北あるいは北海度など北に向かって旅行する時は、藤沢と旅行地で同じ高さの棒が作る影の長さを計って欲しい。 旅行先での影が長くなっていることを体験すれば、地球が丸く緯度差があることを実感できるだろう。 科学を学ぶためは、こうして自分で確かめることがもっと重要だと思う。 (終わり)
|
 戻る
戻る