このレポートは、かたつむりNo.482[2020(令和2)04.19(Sun.)]に掲載されました
 戻る
戻る
| カオス理論〜エドワード・ローレンツのしたこと〜(2) | ||||||||
| 運営委員 山田 佳子 | ||||||||
前回のかたつむりでは、ローレンツが当時のパソコンで「おもちゃの天気」を作ったところまででした。
今回はその「おもちゃの天気」でローレンツが発見したことです。
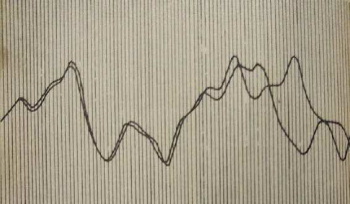
この時、ローレンツは「真空管(当時のコンピュータの部品)が壊れたのか?」と思いました。けれどすぐに自分のミスに気が付きます。 コンピュータのメモリには0.506127という数字が記憶されていたのですが、プリントアウトしたのは紙を倹約するために0.506という数字でした。 その差はわずか0.00127。これは大した誤差ではないと判断したローレンツは0.506を打ち込みました。普通の計算式ならこれくらいの誤差は無視できます。 けれど、ローレンツがコンピュータに計算させていた方程式では、このわずかな誤差が『大異変』につながってしまいました。 はじめに打ち込んだ数字が1/1000違うだけで予想もつかないデータになっていたのです。 これが有名な『バタフライ効果』です。初めの値のわずかな違いが最終的にまったく違うものになってしまいます。例えば、ブラジルでチョウが羽ばたいたとします。 チョウの羽ばたきが起こしたとても小さな風が、テキサス(アメリカの州)に伝わるころにはハリケーンになってしまうくらいの変化が起きてしまうという考え方です。 ローレンツは自分が作った方程式が天気の本質をつかんでいると思っていました。だからそこから「長期天気予報は不可能だ」ということを導き出しました。 とても小さな変化でも、その変化のために予想がつかない結果になってしまうからです。 世界最初のコンピュータを作ったジョン・フォン・ノイマン(1903−1957)は、 人間よりも早く大量に計算ができるコンピュータを使えば天気予報は可能で、いずれは人間が天気を変える時代が来ると考えていました。 しかし、ローレンツはそれが無理だという結論を出しました。実際、現在のスーパーコンピュータを使っても1か月後の藤沢の天気を正確に予報することはできません。 1日先、2日先の予報はなんとかできても、1週間後の予報はあてになりません。また、狭い地域での雷雨や集中豪雨などの予報も難しいです。 気象予報士の「大気が不安定で、ところによっては雨が降るかもしれません」という解説はよく聞きます。 道端のチリを舞わせる小さな風やにわか雨、人工衛星からしか見えない大きな渦などがすべて関わって複雑な動きをするので、天気の予報は難しくなります。 また、人が天気を変えるための行動を起こしたとしても、天気を決める複雑な要素がひとつ増えた程度で、晴れや雨などの変えたかった天気になるとは限りません。 ローレンツはこのようなバタフライ効果を発見しました。けれどそれで終わらせず、さらにそれを徹底的に研究しました。 ローレンツは天気から離れ、天気のように複雑なふるまいをするもっと単純な現象を探しました。そして、ある動作を表す3つの方程式を見つけました。
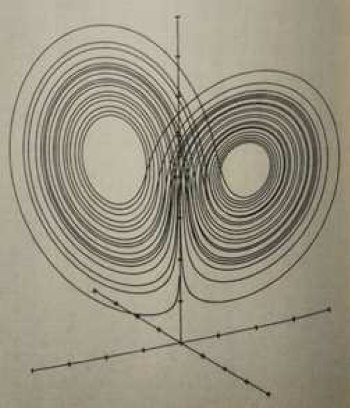
ローレンツが発見した方程式のグラフが右の図です。ローレンツのアトラクタ(集まり)としてとても有名な図です。 どう見ても定規で引けない線で描かれています。チョウの羽のような形ですが、まるい正しい円を描くような繰り返しはしません。 けれど、この二つの手書きのような丸から大きく外れることもしません。 そして、似たような軌道を通っても、一度通った軌道は通らないという信じられない線を描きます。 延々と、似ているけれど同じではない道を動き続けます。これがローレンツが発見した『でたらめさという仮面をかぶった秩序』という幾何学的構造です。 今回はここまでです。 次のかたつむりで、この発見はどう大発見なのかをお伝えします。 参考図書:カオス−新しい科学をつくる,ジェイムズ・グリッグ著,大貫昌子訳,新潮文庫,1991
|
 戻る
戻る